Pythonで競プロしてる 
Nまでの番号が付けられたN個の頂点を持つ根付き木にある条件の操作をしたとき、すべての操作後の各頂点のカウンターの値を求める問題です。
提出
import collections
n, q = map(int, input().split())
ab = [list(map(int,input().split())) for _ in range(n-1)]
px = [list(map(int,input().split())) for _ in range(q)]
cnt = [0]*n
for i in px:
p, x = i
cnt[p-1] += x
hen = [[] for _ in range(n)]
for i in ab:
a, b= i
hen[b-1].append(a-1)
hen[a-1].append(b-1)
qu = collections.deque()
qu.append(0)
ans = [-1]*n
ans[0] = cnt[0]
while qu:
now = qu.popleft()
for i in hen[now]:
if ans[i] != -1:
continue
ans[i] = ans[now]+cnt[i]
qu.append(i)
print(*ans)累積和の進化版のような考え方で解くことができます。
例として、下図のような木を考えていきます。
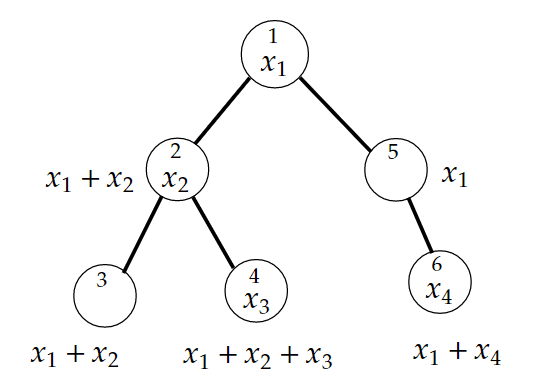
入力をすべて受け取った後、「cnt」のリストを作ります。
「cnt」には、頂点piに足されたxiを加算していきます。
上図の例では、
cnt = [x1, x2, 0, x3, 0, x4]となります。
辺でつながっていて、頂点1に近いほうの頂点を親と考えると、子のカウンターの値は「(親のカウンターの値)+(自分に加算されたcnt)」となります。
これを一番親の頂点1から確かめていく必要があります。
そこで「hen」リストを作成し、各頂点がどことつながっているかをまとめます。
上図では、
hen = [[2, 5], [1, 3, 4], [2], [2], [1, 6], [5]]
# リストに加えるときに、a-1, b-1としているため、実際には、数字に「-1」したものが入っている両端に要素を追加・削除する際に便利な、collectionsモジュールの「deque」を使います。
qu = collections.deque()
qu.append(0)
ans = [-1]*n
ans[0] = cnt[0]
while qu:
now = qu.popleft()
for i in hen[now]:
if ans[i] != -1:
continue
ans[i] = ans[now]+cnt[i]
qu.append(i)まず、quに0を加え、hen[0]に入っている数字を確認します。
hen[0]には、頂点1とつながっている[2, 5](実際には[1, 4])がはいっています。
ans[1] = ans[0]+cnt[1] # x1+x2
ans[4] = ans[0]+cnt[4] # x1より、「ans[1]」「ans[4]」が求まります。
quには、[1, 4]が入るので、次のループでhen[1]をチェックします。
hen[1]には[1, 3, 4](実際には[0, 2, 3])が入っており、これも順番に確かめるわけですが、「ans[0]」の値は「-1」ではないので、これを飛ばします。
ans[2] = ans[1]+cnt[2] # x1+x2
ans[3] = ans[1]+cnt[3] # x1+x2+x3hen[4]には、[1, 6](実際には[0, 5])が入っているため、これをチェックして、
ans[5] = ans[4]+cnt[5] # x1+x4これまでの処理の後、quには[2, 3, 5]が入っていますが、いずれの場合も
if ans[i] != -1:
continueの処理で、ループをスキップしてしまうので、要素の変動はありません。
最終的に
ans = [x1, x1+x2, x1+x2, x1+x2+x3, x1, x1+x4]となるため、これを空白区切りで出力します。
